My current project is an iPad app for designing popup cards – with the goal of making the process easier and more fun. Foldlings allows users to define a sketch of a pop-up in 2D and preview a simulation of their design in 3D, assisting the user in the exploratory process of creating pop-ups. Designs are fabricated by hand or using a laser cutter. Designed and developed with Marissa Allen as our Masters thesis in Computer Science, advised by Emily Whiting. Initial prototype created with Marissa Allen and Tim Tregubov.
Full source available here: https://github.com/harquail/foldlings
You can download the full thesis here. To cite Foldlings in a academic paper, use this link.
Overview
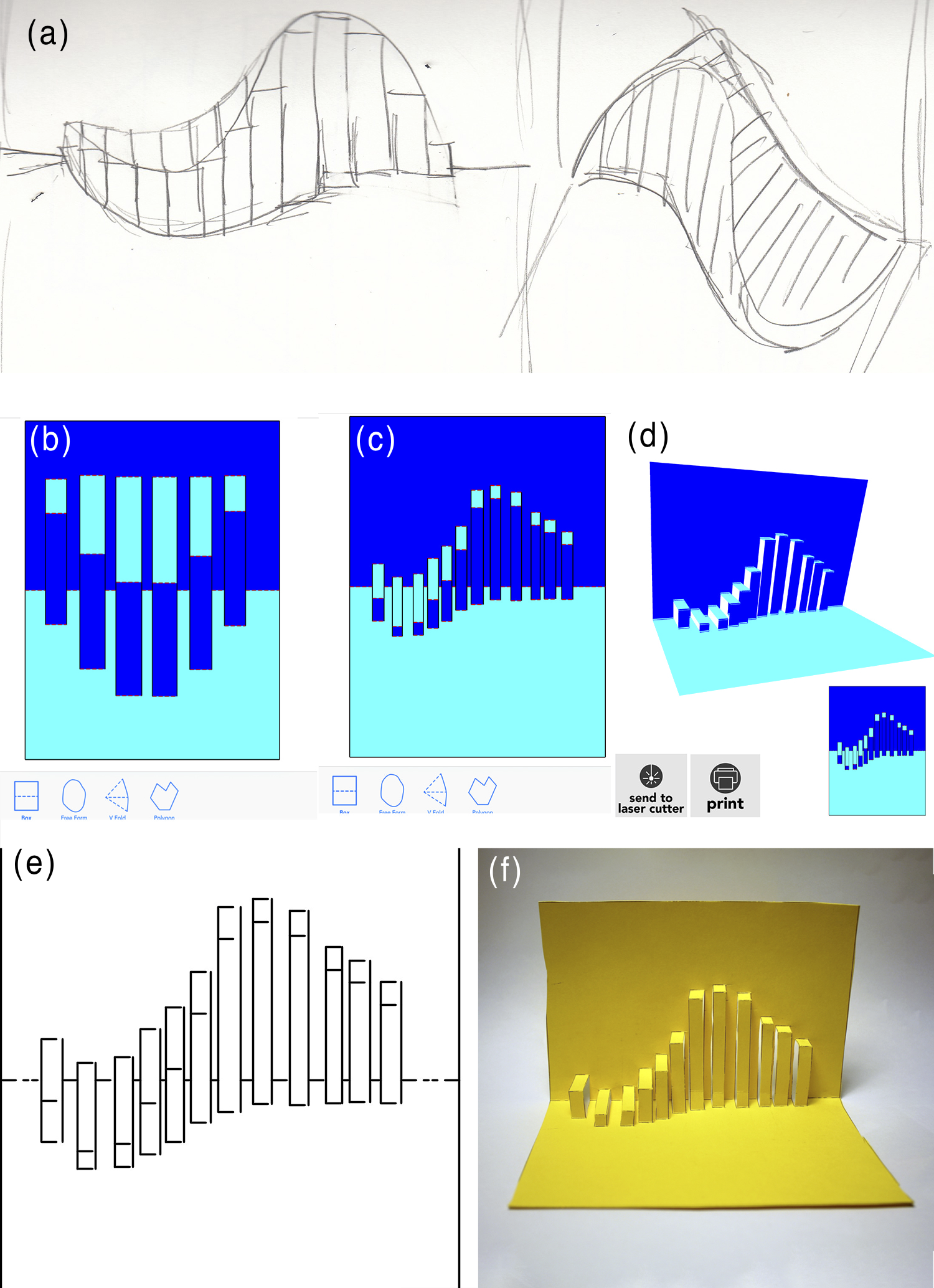
Sample Creations

Creation Pipeline
This shows a user’s design process, starting with concept sketches, and moving through iterations of the sketch using the 3D preview to test the design. Finally, the user exports the design as a fold pattern, and cuts and folds the pop-up card.
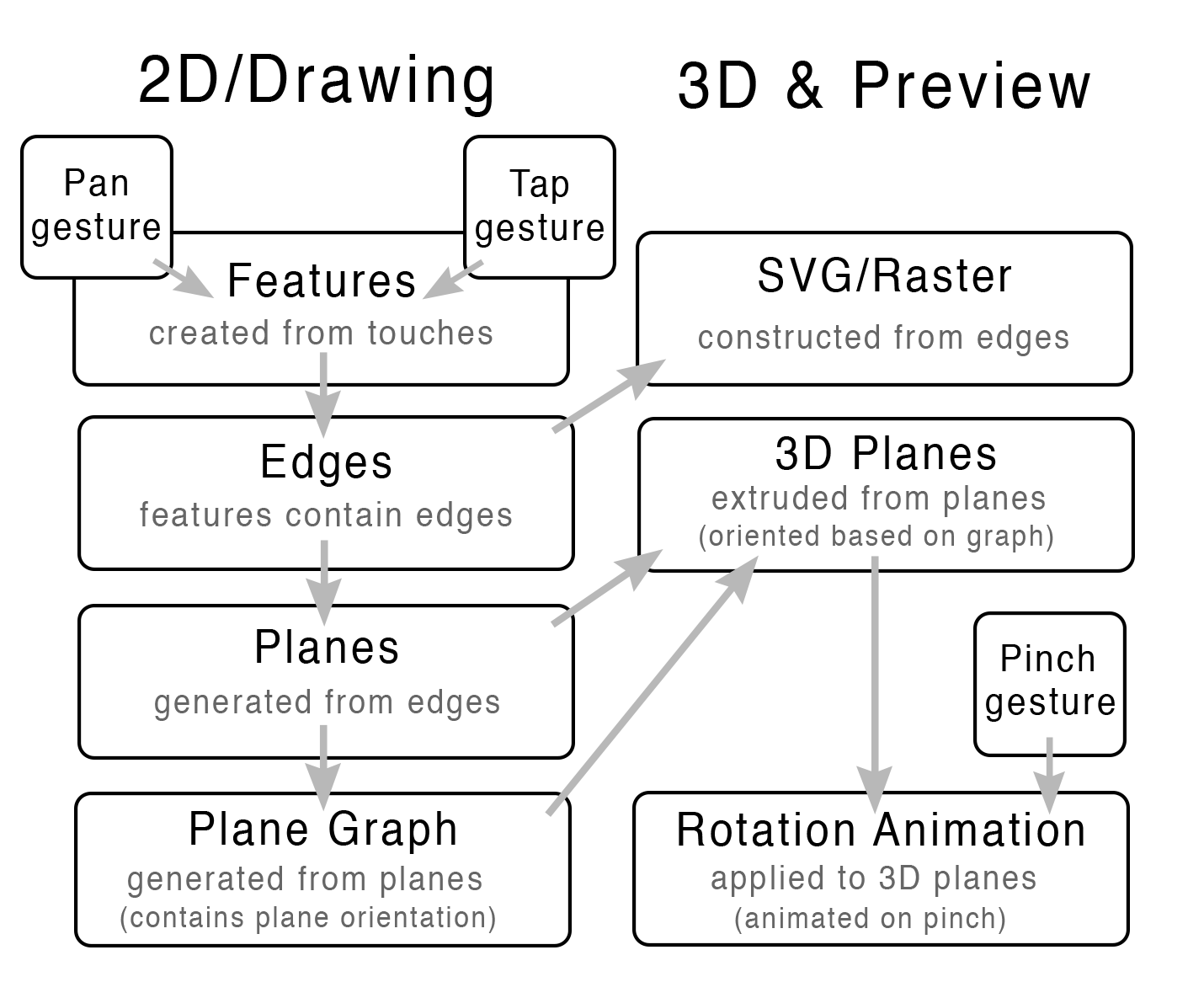
Major Systems
Key data structures and an overview of data flow between systems.
Selected Algorithms
Truncation
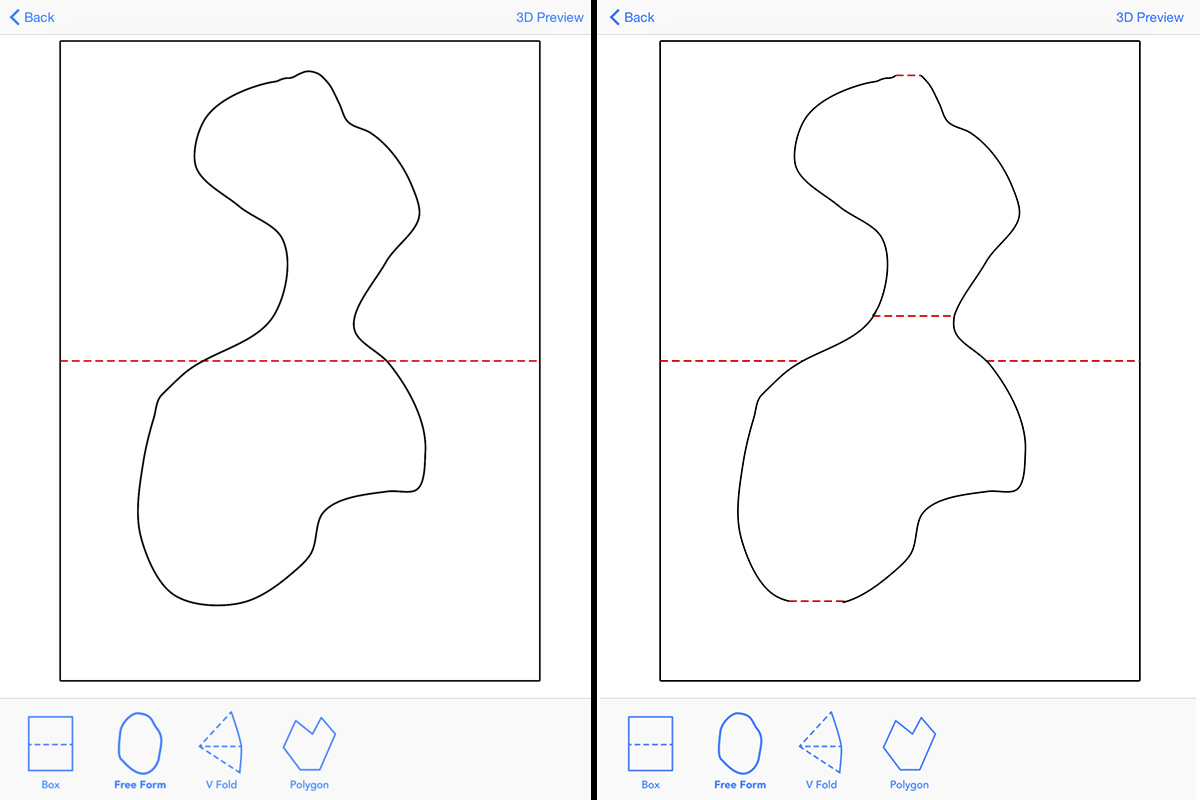
Truncation is the process of converting a closed free-form shape into a valid feature with a driving fold. To truncate a shape, we first find locations for top and bottom folds that will yield folds longer than the minimum edge length. Then, we split the existing path at those intersection points, and remove paths that lie outside the top and bottom folds of the new shape. Thus, we “truncate” the shape, adding horizontal folds and trimming edges that lie outside the new shape.

Split Folds by Occlusion
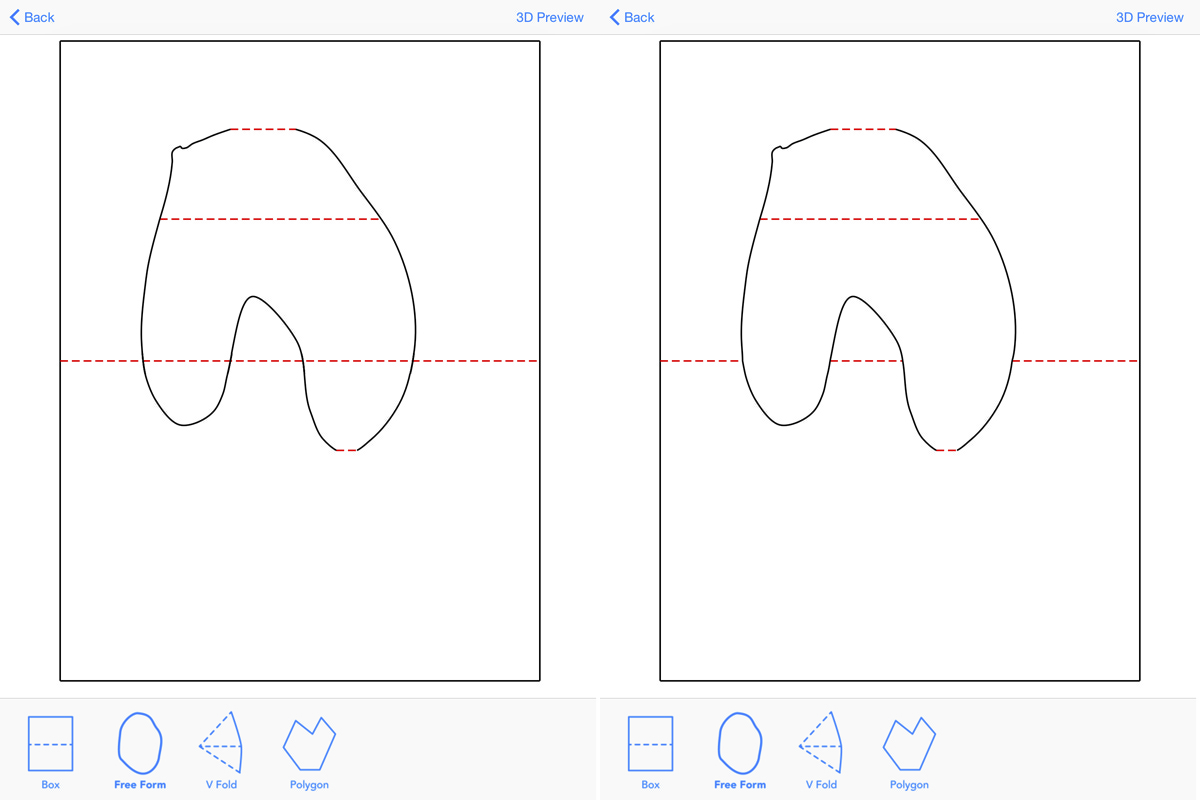
SplitFoldByOcclusion takes as a fold as its input, typically the driving fold for the feature. The function splits the given fold into multiple pieces, removing sections of the edge that would lie inside the bounds of the feature on which the method is called.
Bezier Path Intersection
We use a bitmap approximation of the intersection point between bezier paths, because calculating intersections between arbitrary curves is computationally more expensive. This fast approximation allows us to perform many intersection quickly, minimizing the delay after creating a feature.
After finding the intersection points, we split the existing path at the intersection points. The freeform shape’s path is composed of many cubic bezier curves output by the Catmull-Rom algorithm. In order to split the path, we must first find the closest cubic bezier curve to the intersection point, and then find a value, t within that curve, that gives interpolated position at the intersection point. First, we iterate through all bezier segments in the path, comparing representative points to find the closest curved segment to the intersection point. Within that segment, we recursively subdivide the curve to find a t value very close to the approximated intersection point.
Repairing Self-Intersecting Paths
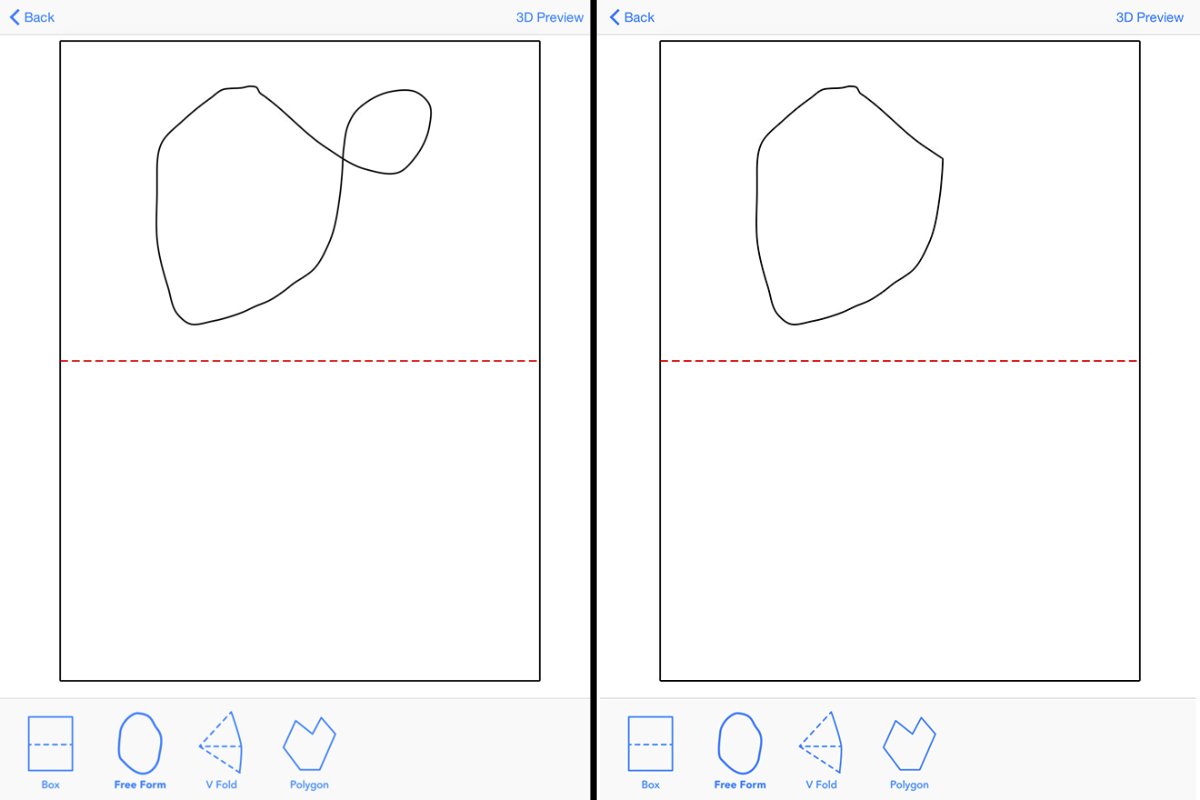
In order to be rendered by SceneKit in 3D, paths cannot have self intersections. Thus, we attempt to repair self-intersecting paths when adding features to the sketch.

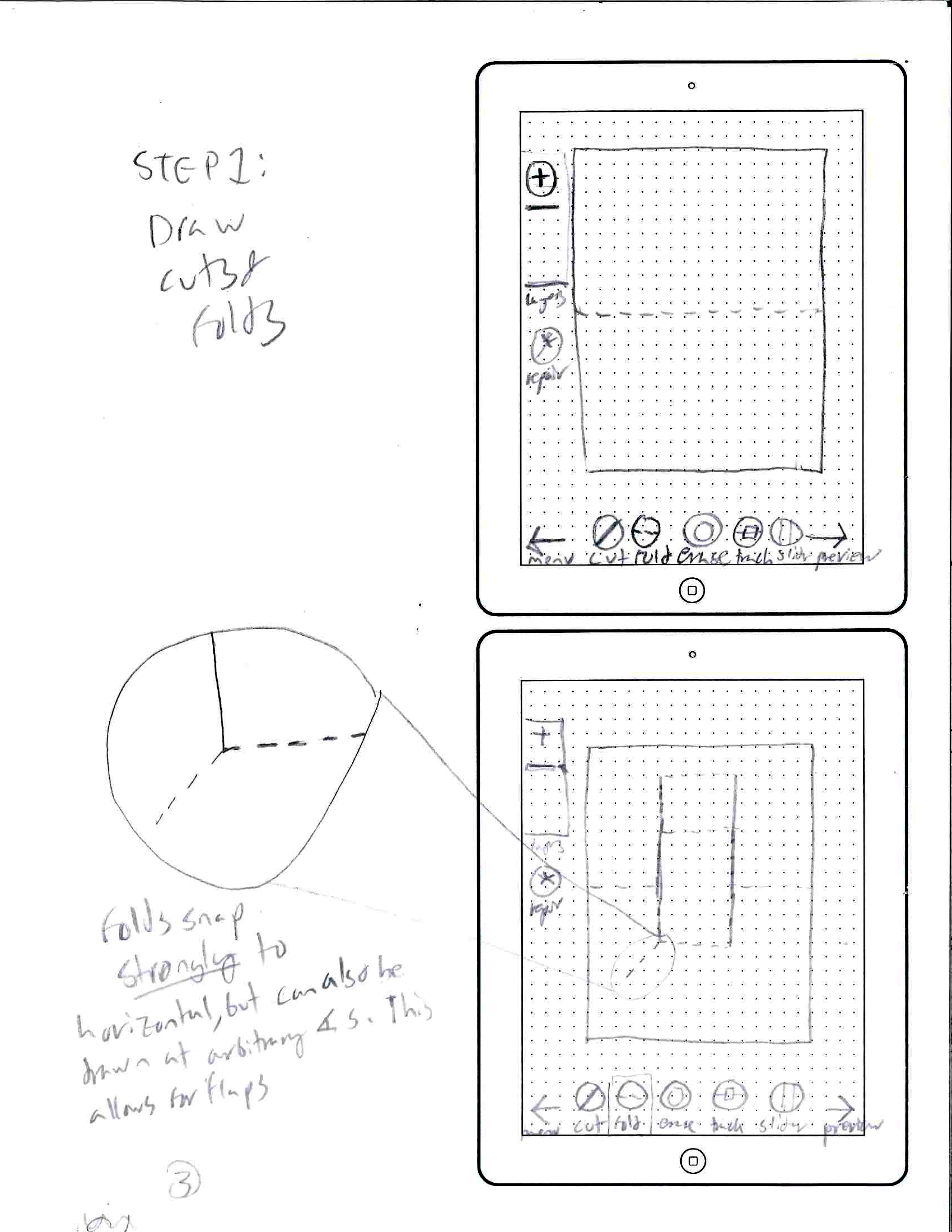
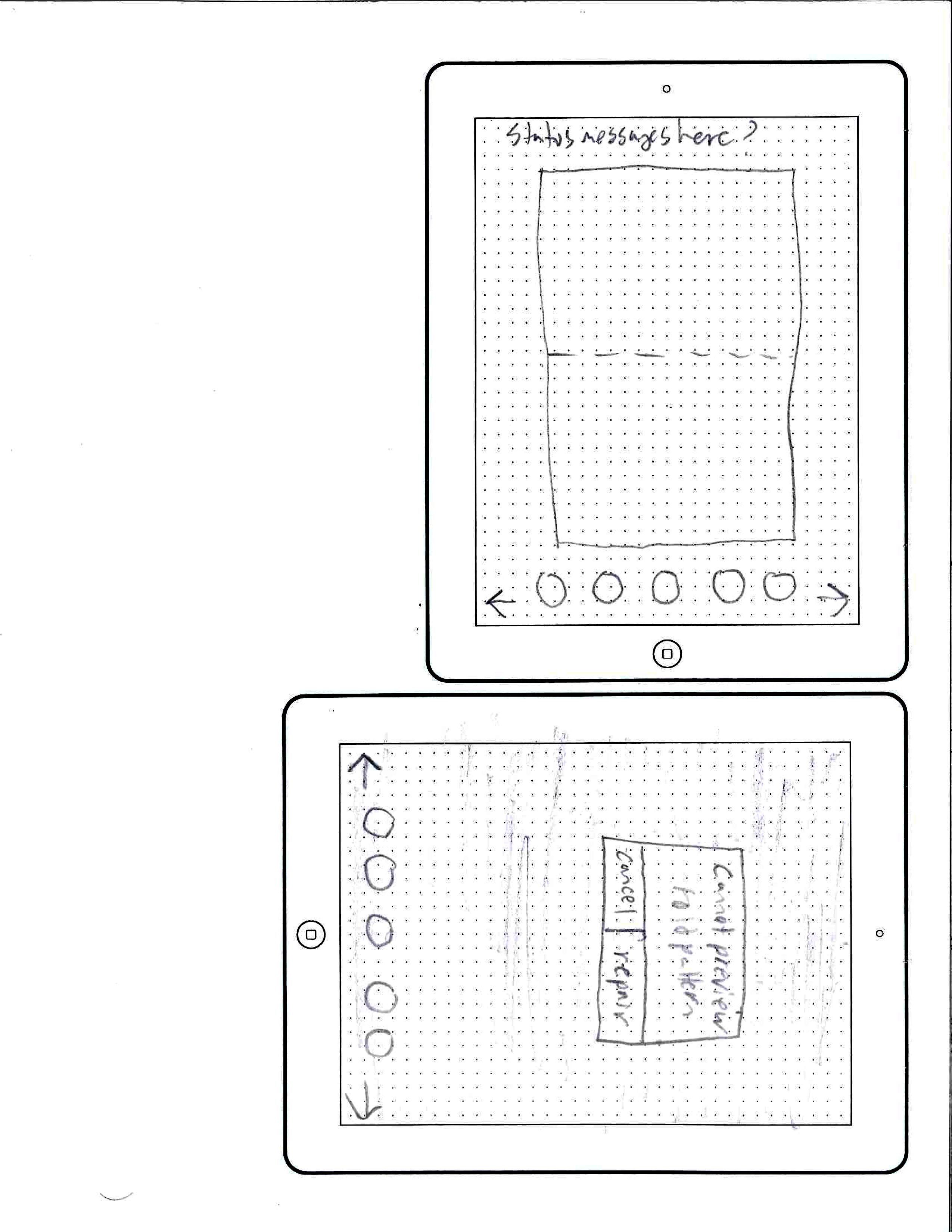
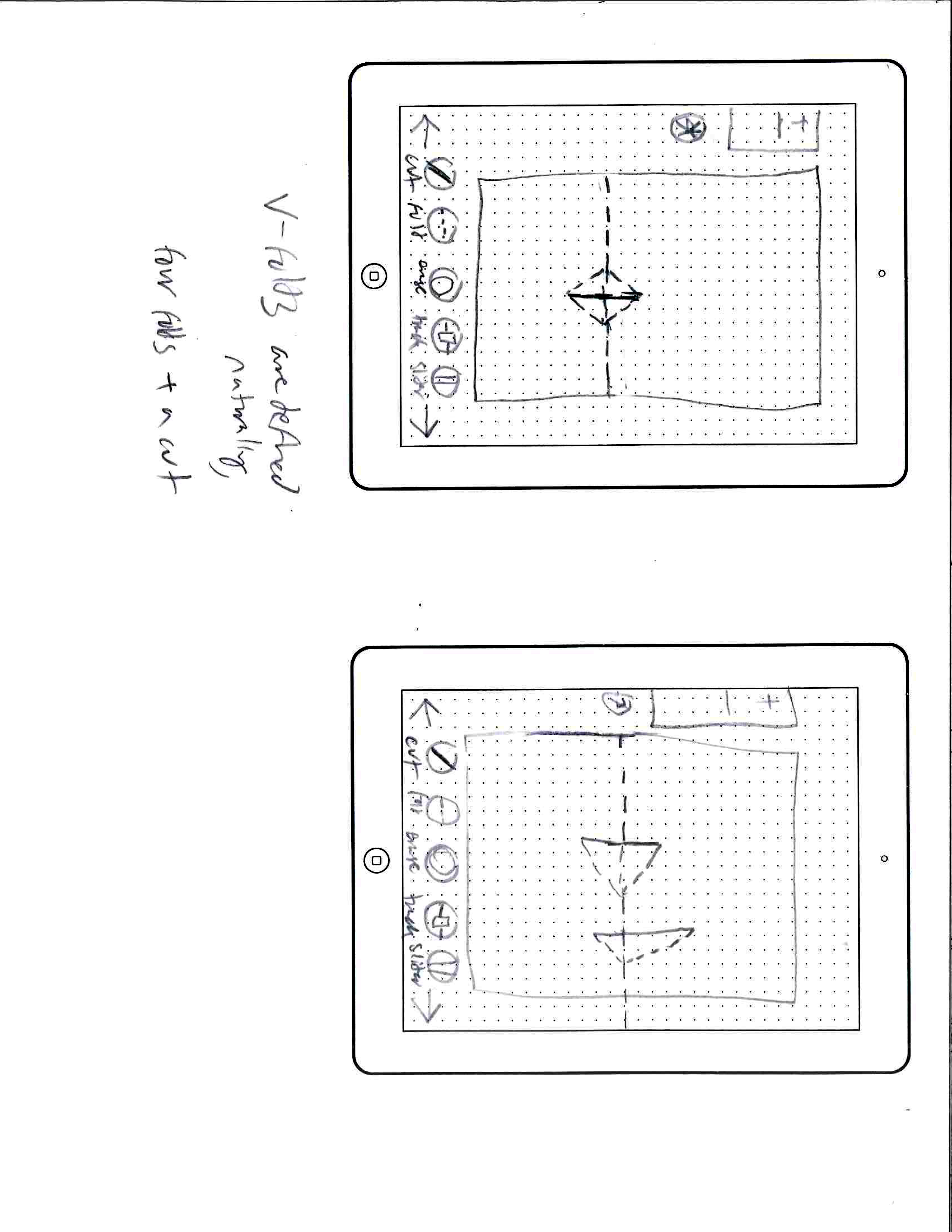
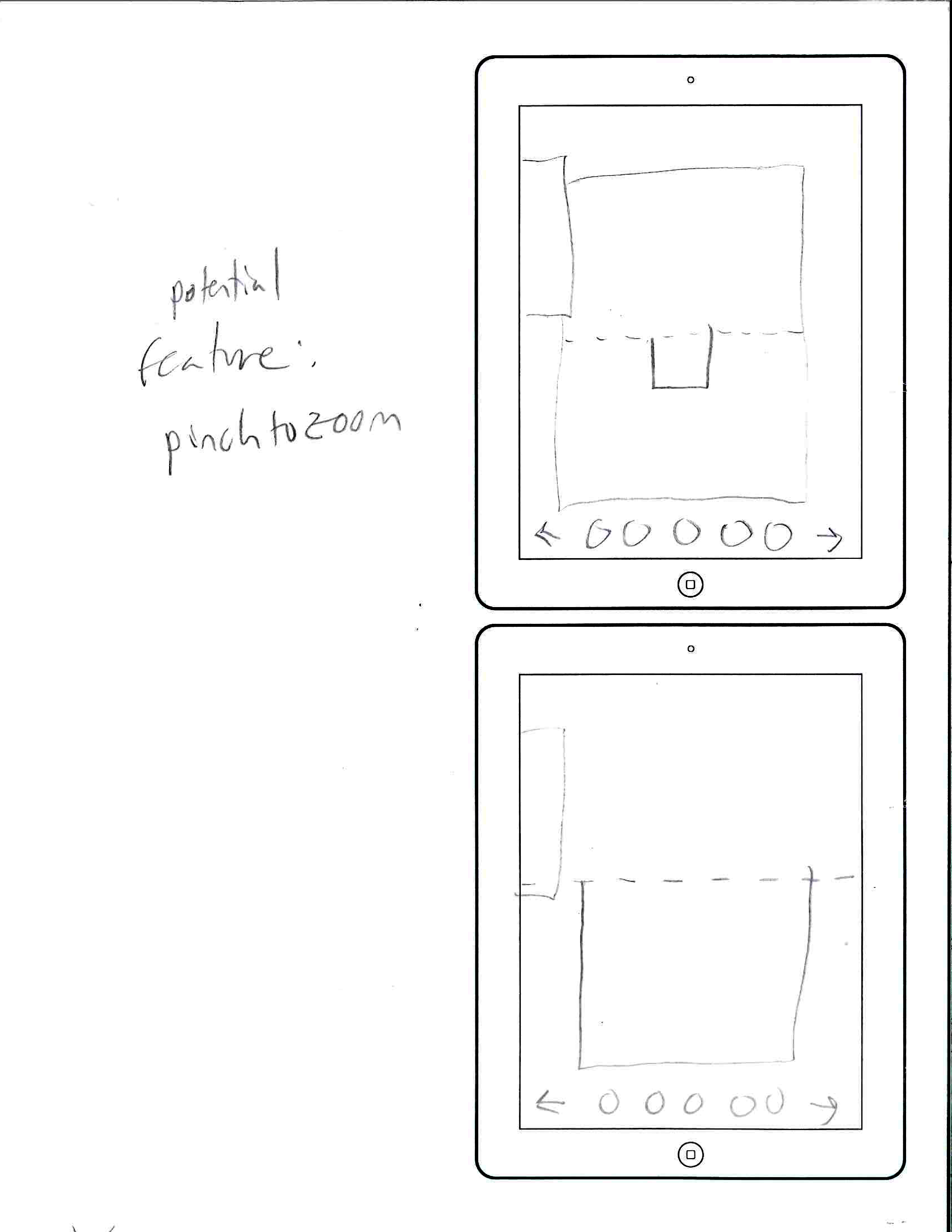
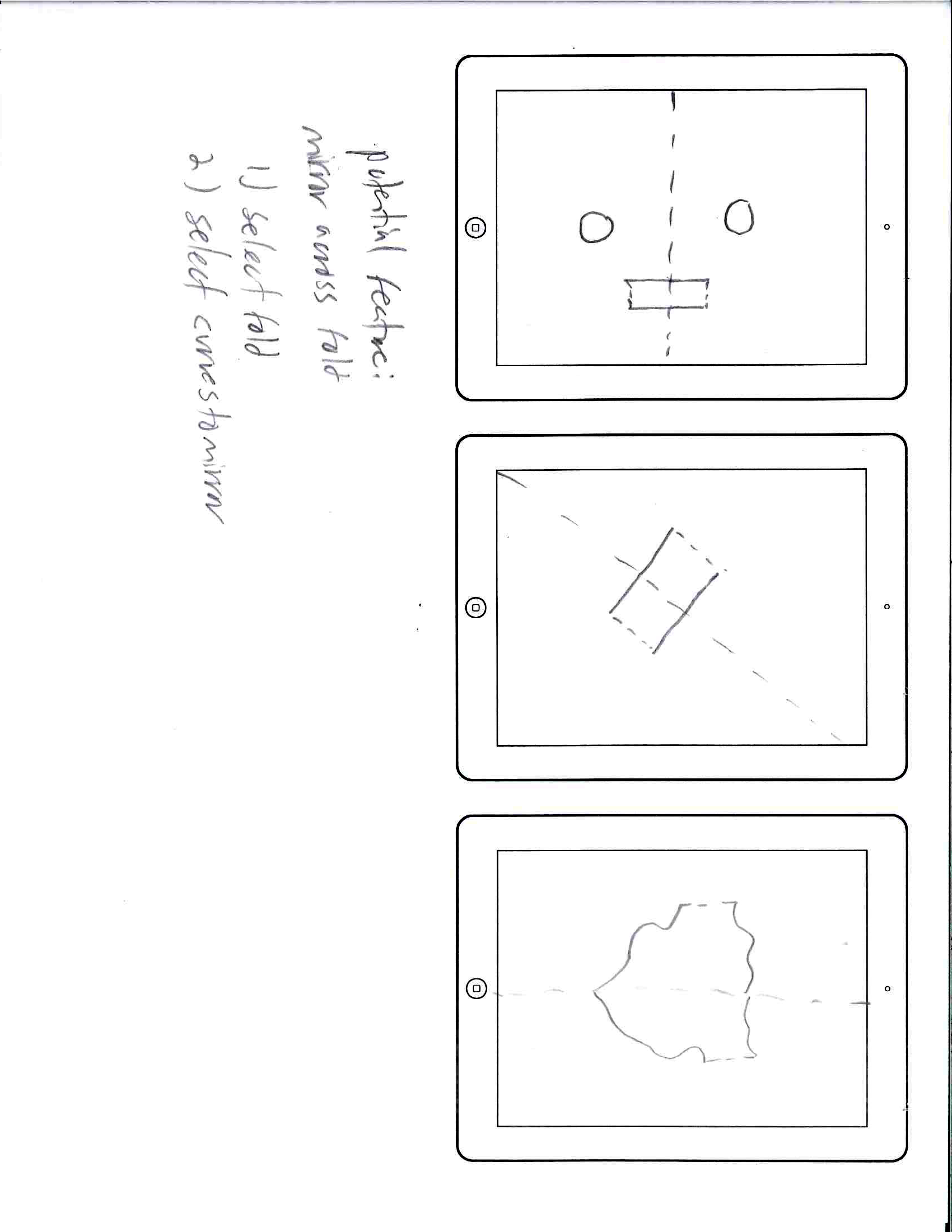
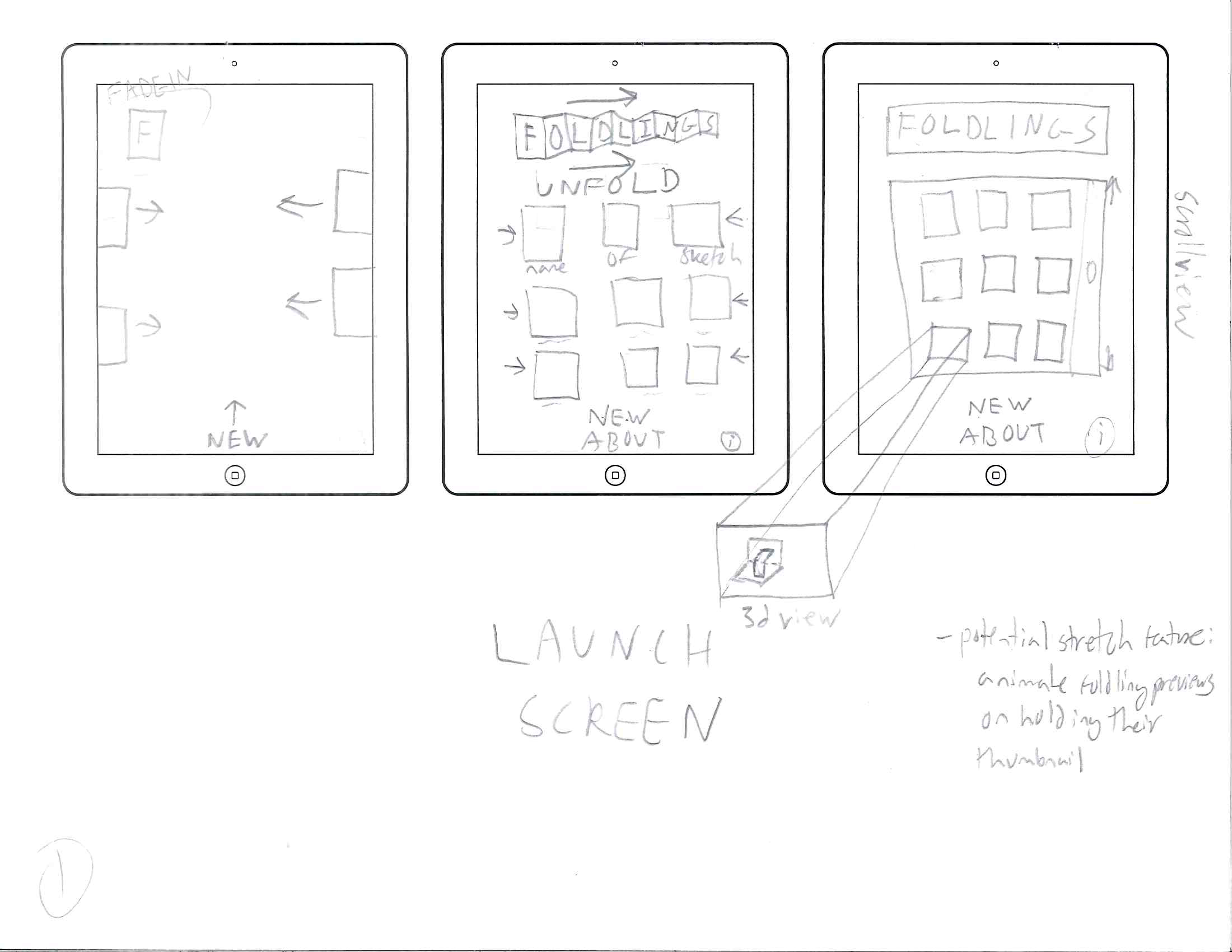
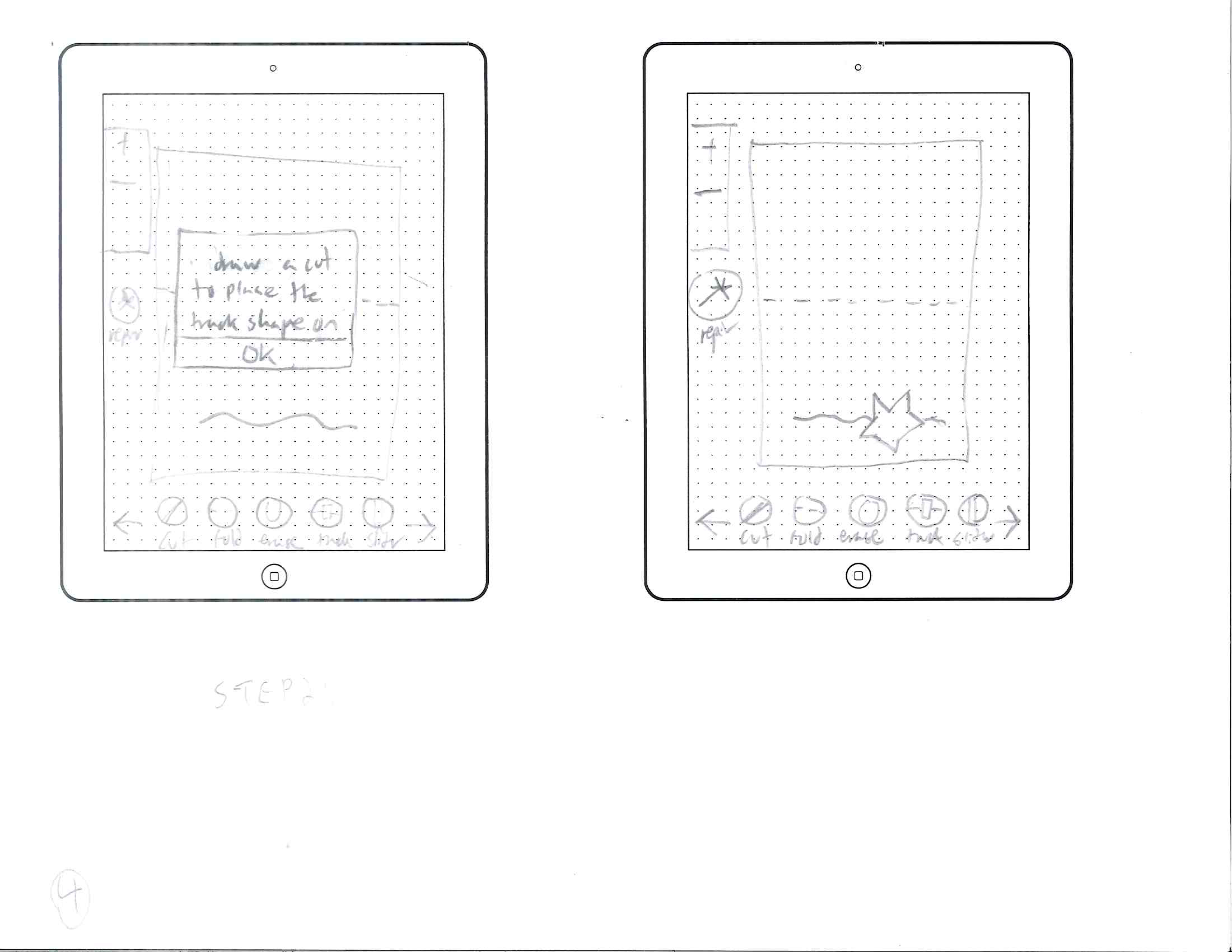
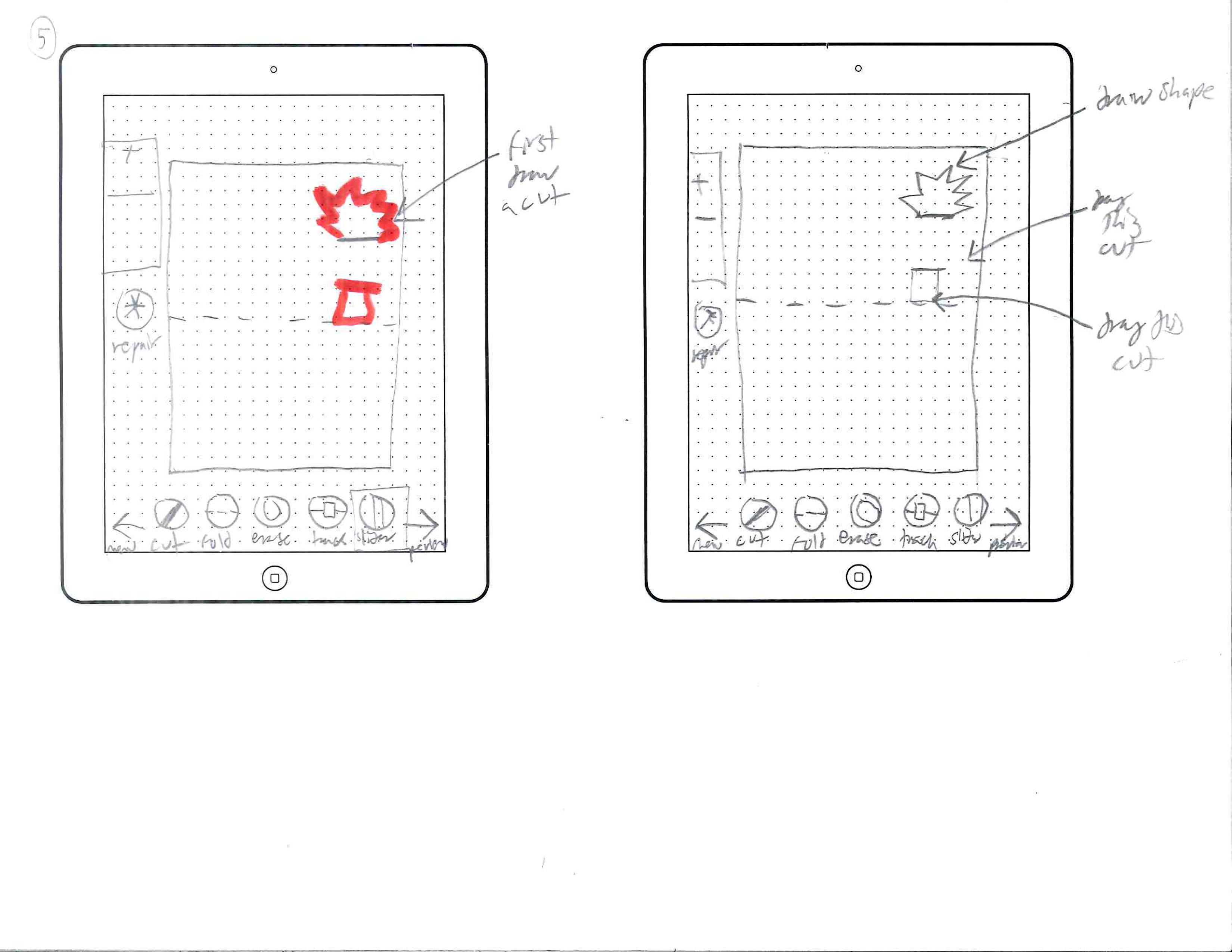
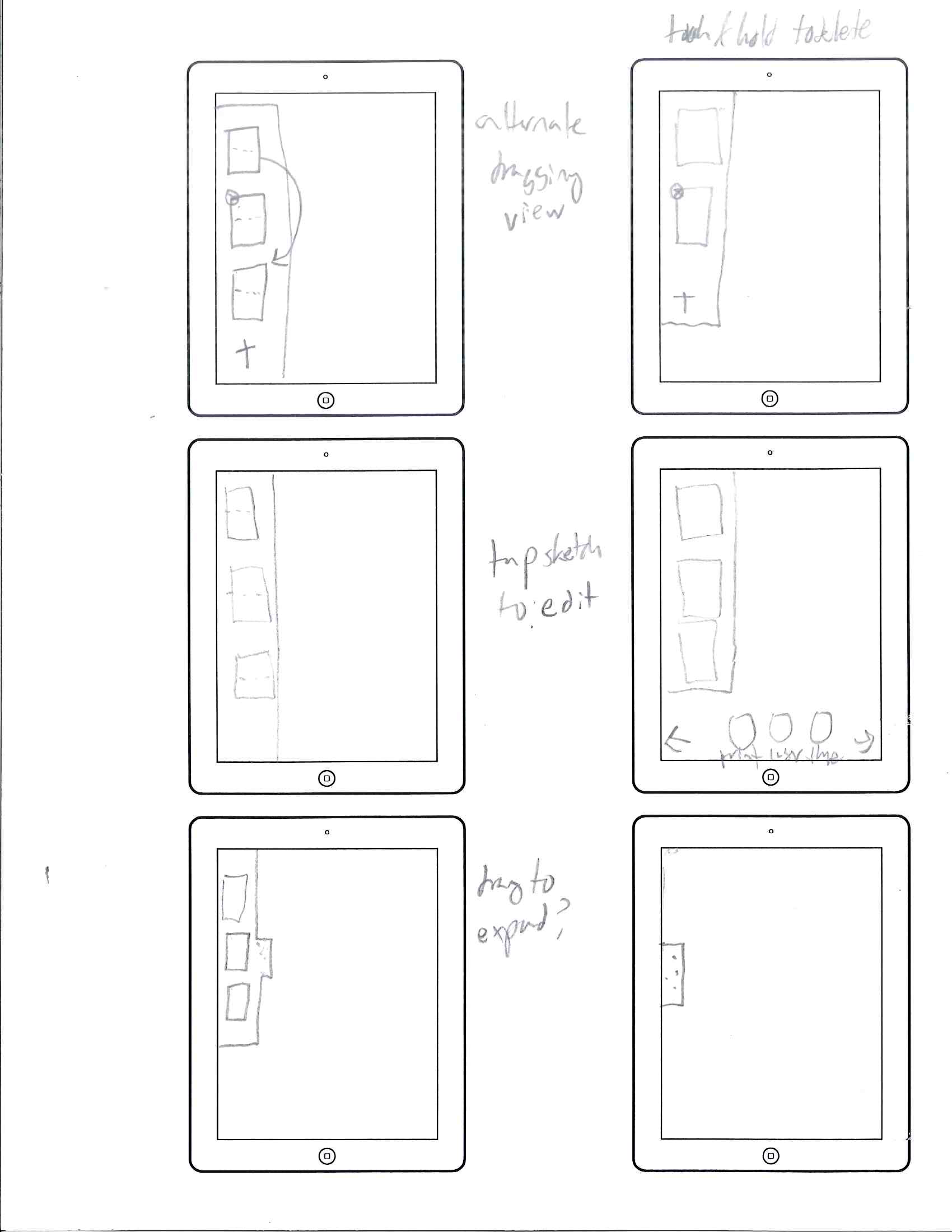
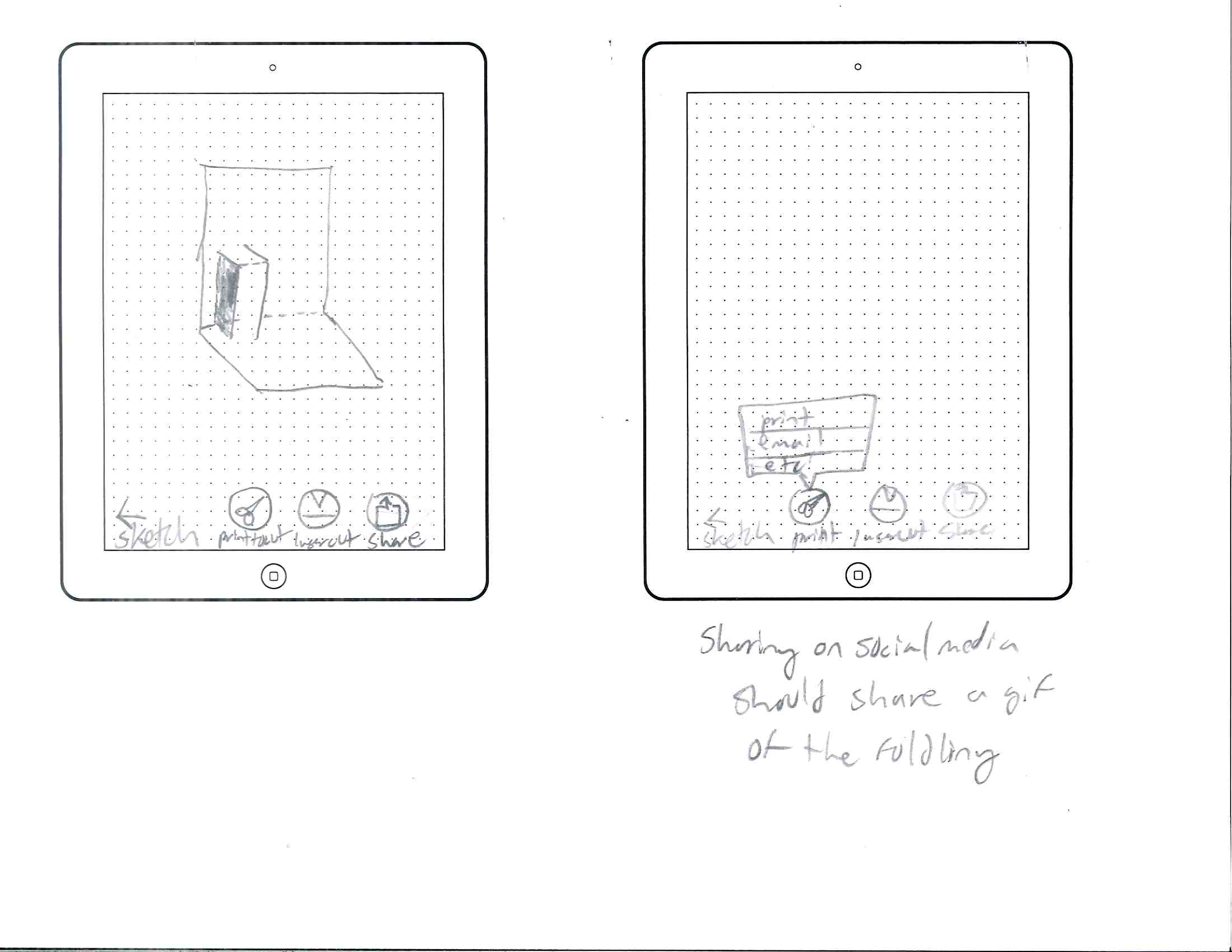
Initial Mockups